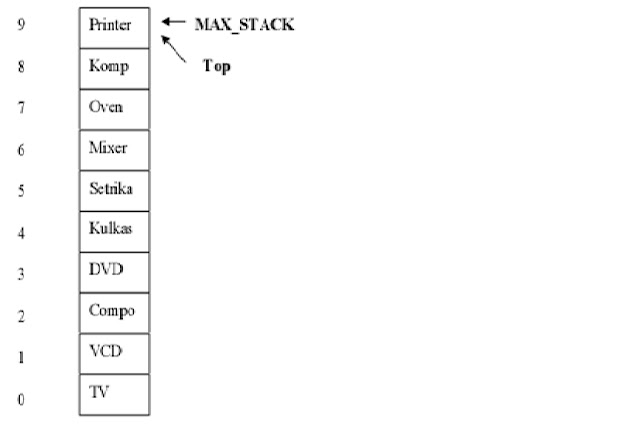
Elemen-elemen yang berada dalam stack, memiliki prinsip paling mendasar dalam pengoperasiannya yaitu prinsip LIFO (Last In First Out) atau elemen yang masuk paling terakhir akan memiliki prioritas untuk keluar paling pertama.
-Overflow : Penambahan elemen > N+1
-Underflow : Pengambilan elemen < 0
Ciri-ciri Stack
-Elemen teratas / puncaknya diketahui.
-Penambahan atau pengambilan elemen stack selalu dilakukan pada elemen teratas stack.
-LIFO (Last In First Out).
Pemanfaatan Stack
-Penghitungan ekspresi matematika (postfix).
-Algoritma Backtracking (runtut balik).
-Algoritma Rekursif.
Operasi-operasi dalam stack :
Create (Stack)
Operasi Create (Stack) digunakan untuk membuat suatu stack baru dengan nama stack, yang nilai elemen saat stack tersebut dibuat 0 dan elemen teratasnya belum ada.
Spesifikasi :
-Input : Stack
-Syarat awal : Tidak ada
-Output : Kosong
-Syarat akhir : Stack dalam keadaan kosong
IsEmpty (Stack)
Operasi ini digunakan untuk memeriksa isi suatu stack dalam keadaan kosong atau tidak. Operasi ini memiliki 2 kondisi boolean, yaitu: True, apabila stack berada dalam kondisi kosong atau nilai elemennya = 0.
False, apabila stack tidak berada dalam kondisi kosong atau nilai elemennya > 0.
Spesifikasi :
-Input : Stack
-Syarat awal : Tidak ada
-Output : Boolean
-Syarat akhir : Sesuai kondisi Boolean di atas
IsFull (Stack)
Operasi ini digunakan untuk memeriksa isi suatu stack dalam keadaan penuh atau tidak.
Spesifikasi :
-Input : Stack
-Syarat awal : Tidak ada
-Output : Boolean
-Syarat akhir : Bernilai True apabila stack dalam keadaan penuh
Push (Stack, Elemen)
Operasi ini digunakan untuk menambahkan sebuah elemen dengan nilai X pada puncak suatu stack, sehingga posisi paling atas stack bernilai X, penerapan operasi Push pada suatu Stack(S) akan berakibat Overflow apabila nilai stack tersebut telah lebih dari maksimum.
Spesifikasi :
-Input : Stack dan elemen baru
-Syarat awal : Stack tidak penuh
-Output : Stack
-Syarat akhir : Stack bertambah satu elemen
Pop (Stack)
Operasi ini digunakan untuk menghapus elemen teratas sebuah stack, sehingga jumlah nilai stack akan berkurang satu elemen dan nilai teratas stack akan berubah. Operasi Pop dapat menyebabkan kondisi Underflow apabila suatu stack telah berada dalam kondisi minimum saat dilakukan operasi Pop.
Spesifikasi :
-Input : Stack
-Syarat awal : Stack tidak dalam kondisi kosong
-Output : Stack dalam informasi Pop
-Syarat akhir : Stack berkurang satu elemen
Clear (Stack)
Operasi ini digunakan untuk mengosongkan stack (membuat nilainya menjadi 0).
Top of Stack
Operasi ini digunakan untuk mengetahui elemen teratas pada sebuah stack.
Operand dan Operator
Infix, Prefix ataupun Postfix adalah bentuk penulisan operasi matematika, bedanya :
Infix Operator diletakkan di antara Operand
Prefix Operator diletakkan di depan Operand
Postfix / Sufix Operator diletakkan di belakang Operand
Mengapa harus menggunakan Prefix dan Postfix?
Karena infix memiliki beberapa kekurangan, yaitu :
Urutan pengerjaan tidak berdasarkan letak kiri atau kanannya, tetapi berdasarkan precedence-nya
Contoh : 3 + 4 x 2
3 + 4 x 2, maka urutan pengerjaan adalah 4 x 2 dahulu.
3 + 8 , baru hasilnya ditambah 3
11
Urutan precedence (dari prioritas tertinggi) adalah sebagai berikut :
-Pemangkatan
-Perkalian dan Pembagian
-Penjumlahan dan Pengurangan.
-Kecuali kalau ada tanda kurung.
Menggunakan tanda kurung. Infix bisa menggunakan tanda kurung. Tetapi tanda kurung dapat mengacak urutan precedence.
Contoh : Tanpa penggunaan tanda kurung :
9 – 5 – 3
9 – 5 – 3 , maka urutan pengerjaan adalah 9 - 5 dahulu.
4 – 3
1
Bandingkan dengan penggunaan tanda kurung berikut :
9 – ( 5 – 3 )
9 – ( 5 – 3 ), maka urutan pengerjaan adalah 5 – 3 dahulu.
9 – 2
7
Jika suatu program akan mengevaluasi (mencari hasil) suatu infix, maka komputer perlu men-scan berulang-ulang mencari urutan pengerjaannya dahulu.
Contoh : 7 + 4 x 2 – 6 / 3
Jika kita diminta untuk menghitung soal seperti itu, maka kita tahu bahwa yang pertama kali harus kita kerjakan adalah 4 x 2. Lalu 6 / 3 dsb, seperti langkah-langkah berikut :
7 + 4 x 2 – 6 / 3
7 + 8 – 6 / 3
7 + 8 – 2
15 – 2
13
Komputer tidak bisa membaca keseluruhan soal sekaligus. Komputer hanya bisa men-scan soal satu per satu operand atau operator. Jadi langkah- langkah si komputer dalam mengerjakan soal infix seperti berikut:
-Cari precedence tertinggi dengan men-scan kiri ke kanan keseluruhan soal.
-Hitung nilai operator dengan precedence tertinggi tersebut.
-Ulangi lagi dari langkah 1, sampai semua operator selesai dikerjakan.
Jika komputer tidak men-scan keseluruhan soal terlebih dahulu, maka akan terjadi kesalahan pada hasilnya.
Konversi.
Infix -> Prefix Manual
Langkah-langkahnya:
-Cari operator yang memiliki precedence tertinggi.
-Letakkan operator tsb di depan operand-operandnya.
-Ulangi lagi.
Contoh:
A + B – C x D ^ E / F , ”D ^ E” maksudnya D pangkat E.
A + B – C x D ^ E / F , pangkat memiliki precedence tertinggi
A + B – C x ^ D E / F , taruh ^ di depan D dan E
A + B – C x ^ D E / F , x (kali) dan / (bagi) memiliki precedence sama tapi x di kiri
A + B – x C ^ D E / F , taruh x di belakang
A + B – x C ^ D E / F , dan sebagainya
A + B – / x C ^ D E F
A + B – / x C ^ D E F
+ A B – / x C ^ D E F
+ A B – / x C ^ D E F
– + A B / x C ^ D E F , inilah bentuk Prefix-nya.
Infix -> Postfix Manual
Langkah-langkahnya :
-Cari operator yang memiliki precedence tertinggi.
-Letakkan operator tsb di belakang operand-operandnya.
-Ulangi terus sampai bosan, eh salah, sampai selesai.
Contoh:
A + B – C x D ^ E / F , ”D ^ E” maksudnya D pangkat E.
A + B – C x D ^ E / F , pangkat memiliki precedence tertinggi
A + B – C x D E ^ / F , taruh ^ di belakang D dan E
A + B – C x D E ^ / F , x (kali) dan / (bagi) memiliki precedence sama tapi x di kiri
A + B – C D E ^ x / F , taruh x di belakang
A + B – C D E ^ x / F ,dan sebagainya
A + B – C D E ^ x F /
A + B – C D E ^ x F /
A B + – C D E ^ x F /
A B + – C D E ^ x F /
A B + C D E ^ x F / – , inilah bentuk Postfix-nya.
Infix -> Prefix Menggunakan Stack
Kali ini kita menggunakan 2 Stack, yang satu untuk menampung operand (sebut saja dengan Stack “Pre”) dan yang satunya lagi untuk menampung operator (sebut saja dengan Stack “Opr”).
Langkah – langkah :
-Scan Infix dari kanan ke kiri.
-Jika berupa operand, maka Push ke Stack “Pre”.
-Jika berupa operator, maka bandingkan operator NEW tersebut dengan TOP pada Stack “Opr”:
+WHILE precedence TOP > NEW, maka POP Stack “Opr” pindahkan ke Stack “Pre”.
+Lalu Push NEW ke dalam Stack “Opr”.
-Jika berupa “)“, maka Push “)“ ke Stack “Opr”.
-Jika berupa “(”, maka Pop Stack “Opr” pindahkan ke stack “Pre” sampai ketemu “)“.
-Ulangi terus dari langkah 1 sampai seluruh Infix sudah di-scan.
-POP semua isi Stack “Opr”, pindahkan ke Stack “Pre”.
-POP semua isi Stack “Pre”, pindahkan ke Prefix.
Keterangan :
Setelah Stack “Opr” dikosongkan. Jangan lupa untuk memindahkan isi Stack “Pre” ke Prefix. Sehingga urutan peletakkan operand pada hasil akhirnya tetap sama (Infix diubah ke Postfix ataupun Prefix, urutan letak operand-nya tetap sama).
Infix -> Postfix Menggunakan Stack
Cara pembuatan :
-Scan Infix dari kiri ke kanan.
-Jika berupa operand, maka tulis di Postfix.
-Jika berupa operator, maka bandingkan operator NEW tsb dgn TOP pada Stack :
+WHILE precedence TOP >= NEW, maka POP Stack pindahkan ke Postfix.
+Lalu Push NEW ke dalam Stack.
-Jika berupa “(“, maka Push “(“ ke Stack.
-Jika berupa “)”, maka Pop Stack pindahkan ke Postfix sampai ketemu “(“.
-Ulangi terus dari langkah 1 sampai seluruh Infix sudah di-scan.
-POP semua isi Stack, pindahkan ke Postfix.
-Perlu diingat !! tanda kurung “(“ ataupun “)” tidak dimasukkan ke Postfix.
Keterangan :
Tanda kurung “(“ dan “)”, dapat dianggap tidak memiliki precedence, sehingga pada langkah ke-7, operator “–“ tidak perlu dibandingkan lagi dengan “(“ dan langsung di Push ke Stack.
Pada langkah ke-8, tanda “)” dibaca dari Infix, maka Stack di Pop terus sampai ketemu tanda “(“. Sehingga pada contoh di atas operator “–“ di Pop dan dipindahkan ke Postfix.
Evaluasi.
Yang dimaksud dengan “Evaluasi” disini adalah mencari nilai akhir dari suatu notasi. Dengan kata lain, disuruh ngitung hasilnya.
Contoh : Berapa hasil 3 + 4 ?
Jawab : 7
Evaluasi Postfix Manual
Langkah-langkahnya :
-Scan Postfix dari kiri ke kanan.
-Jika berupa operand, cuekin dulu aja.
-Jika berupa operator, ambil 2 operand sebelumnya (yang tadi sempet kita cuekin di sebelah kiri), lakukan perhitungan, lalu simpan lagi berupa operand.
-Begitu seterusnya sampai ujung kanan Postfix.
Contoh :
Postfix : 7 6 5 x 3 2 ^ – +
7 6 5 x 3 2 ^ – + , scan terus sampai ketemu operator pertama.
7 6 5 x 3 2 ^ – + , hitung 6 x 5.
7 30 3 2 ^ – + , scan lagi cari operator berikutnya.
7 30 3 2 ^ – + , hitung 3 pangkat 2.
7 30 9 – + , scan lagi cari operator berikutnya.
7 30 9 – + , hitung 30 – 9.
7 21 + , scan lagi.
7 21 + , hitung 7 + 21.
28 , selesai.
Evaluasi Prefix Manual
Langkah-langkahnya idem, sama kaya Postfix, tapi arah scannya dari kanan ke kiri.
Contoh :
Prefix : + 7 – x 6 5 ^ 3 2 (soalnya sama nih sama soal Postfix tadi)
+ 7 – x 6 5 ^ 3 2 , scan kanan ke kiri sampai ketemu operator.
+ 7 – x 6 5 ^ 3 2 , hitung 3 pangkat 2.
+ 7 – x 6 5 9 , selanjutnya silahkan pelajari sendiri dulu.
+ 7 – x 6 5 9
+ 7 – 30 9
+ 7 – 30 9
+ 7 21
+ 7 21
28.
Selesai.